Общие сведения
В природе существует несколько видов силовых полей. Одним из них является магнитное поле (МП). В физике под ним понимают силу, действующую на перемещающиеся электрические заряды, обладающие магнитным моментом. Каждое тело в том или ином виде характеризуется восприимчивостью к такого роду полю.
Для понимания процесса можно провести эксперимент. Если взять кольцо индуктивности и пропустить через него электрический ток, то вокруг него возникнет электромагнитное поле. Если в катушку вставить железный сердечник, то магнитные свойства усилятся. Другими словами, железо усиливает магнитное поле, созданное током, протекающим по виткам. Получается, что появляется дополнительный источник магнетизма — железо. По принципу суперпозиции векторы источников складываются. Возникает усиленное поле.
Допустим, магнитная индукция поля, создаваемая только током, имеет величину B0, а веществом — B1. Вектор магнитной индукции в материале будет складываться из этих двух величин: B = B0 + B1. Основываясь на эксперименте, физики решили ввести новую величину, которая характеризует, насколько вещество изменяет магнитное поле. Этот параметр было решено обозначить символом μ и назвать магнитной проницаемостью. Её единицей измерения стала безразмерная величина.
Таким образом, физический смысл магнитной проницаемости вещества заключается в величине, равной отношению модуля вектора магнитной индукции поля в материале к создаваемому теми же токами полю без дополнительных элементов. Для вакуума формула магнитной проницаемости имеет вид μ = B / B0. По сути параметр является магнитным аналогом диэлектрической проницаемости. Но если диэлектрики всегда ослабляют поле, то магнетики его усиливают.
На протяжении нескольких десятков лет различные физики проводили эксперименты над способностью материалов поддерживать распространение МП. В результате была построена таблица, в которую были занесены показатели, характерные для разных сред. Так, для воздуха параметр равняется 1.25663753*10−6, вакуума — 4π*10−7, дерева — 1.25663760*10−6, а чистого железа — 6.3*10−3. Все эти данные общедоступны. Их легко можно найти практически в любом физическом справочнике.
Магнитная проницаемость основных материалов, таблица.
- Магнитная проницаемость — это способность материала поддерживать распростарнение магнитного поля в нем.
- Магнитная проницаемость измеряется в Гн/м = (H/m (henries/m)) или Н/А2 = (N/A2 (newtons/ampere2)
- Магнитная проницаемость вакуума = Магнитная постоянная это:
- µ0 = 4π*10−7 (Гн/м) ≈ 1.257*10−6 (H/m, N/A2)
Относительнаямагнитная проницаемость материала (случается ее называют просто «магнитной проницаемостью») это: отношение магнитной проницаемости среды к магнитной проницаемости вакуума µ0:
- µr = µ / µ0
- где
- µr = относительная магнитная проницаемость материала (среды)
- µ =магнитная проницаемость материала (среды)
MediumPermeability- µ — (Гн/м) Relative permeabilityμ / μ0
| Воздух | 1.25663753*10−6 | 1.00000037 |
| Алюминий | 1.256665*10−6 | 1.000022 |
| Аустенитная нержавеющая сталь | 1.260*10−6 — 8.8*10−6 | 1.003–7 |
| Вакуум (µ0) | 4π*10−7 | 1 |
| Вода | 1.256627*10−6 | 0.999992 |
| Водород | 1.2566371*10−6 | 1 |
| Висмут | 1.25643*10−6 | 0.999834 |
| Дерево | 1.25663760*10−6 | 1.00000043 |
| Железо (чистота 99.8%) | 6.3*10−3 | 5000 |
| Железо (99.95% чистое Fe отожженное в водороде) | 2.5*10−1 | 200000 |
| Железо-кобальтовые сплавы | 2.3*10−2 | 18000 |
| Медь | 1.256629*10−6 | 0.999994 |
| Никель-цинковый феррит — магнит | 2.0*10−5 – 8.0*10−4 | 16 – 640 |
| Мартенситная нержавеющая сталь (отожженная) | 9.42*10−4 — 1.19*10−3 | 750 – 950 |
| Мартенситная нержавеющая сталь (закаленная) | 5.0*10−5 — 1.2*10−4 | 40 – 95 |
| NANOPERM® — магнитомягкий нанокристаллический сплав | 1.0*10−1 | 80000 |
| Неодимовый магнит | 1.32*10−6 | 1.05 |
| Никель | 1.26*10−4 — 7.54*10−4 | 100 – 600 |
| Пермаллой (сплав 80% никеля и 20% железа) | 1.0*10−2 | 8000 |
| Платина | 1.256970*10−6 | 1.000265 |
| Сарфир | 1.2566368*10−6 | 0.99999976 |
| Сверхпроводники | 0 | 0 |
| Углеродистая сталь | 1.26*10−4 | 100 |
| Ферритная нержавеющая сталь (отожженная) | 1.26*10−3 — 2.26*10−3 | 1000 – 1800 |
| Фторопласт 4, Ф-4, Teflon | 1.2567*10−6 | 1 |
Относительная магнитная проницаемость среды
Относительная магнитная проницаемость среды описывает во сколько раз индукция данного магнитного поля в данной среде отличается от индуции этого же поля в вакууме.
Относительная магнитная проницаемость среды обозначается μr или просто μ.
Относительная магнитная проницаемость среды является безразмерной величиной.
Относительная магнитная проницаемость для ферромагнитных материалов зависит от изменения магнитного поля. Для прочих материалов относительная магнитная проницаемость примерно равна единице и постоянна.
Магнитная восприимчивость вещества
Обычно связь вектора намагниченности J→ и вектора напряженности в каждой точке магнетика обозначается:
J→=χH→.
Определение 2
χ является магнитной восприимчивостью. Величина безразмерная. Если вещество неферромагтиное и обладает небольшим полем, то χ не зависит от напряженности, является скалярной величиной.
Анизотропные среды предполагают χ в качестве тензора, направления J→ и H→ не совпадают.
Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать задание
Связь между магнитной восприимчивостью и магнитной проницаемостью
Из определения вектора напряженности магнитного поля:
H→=B→μ0-J→.
При подстановке выражения J→=χH→ в H→=B→μ0-J→ получаем:
H→=B→μ0-H→.
Напряженность приобретает вид:
H→=B→μ01+χ→B→=μ0(1+χ)H→.
При сравнении B→=μμ0H→ и H→=B→μ01+χ→B→=μ0(1+χ)H→:
μ=1+χ.
Магнитная восприимчивость может принимать как положительные, так и отрицательные значения. Из μ=1+χ имеем, что μ может быть больше или меньше 1.
Пример 1
Произвести вычисление намагниченности в центре кругового витка с радиусом R=0,1 м и током I=2 А при погружении в жидкий кислород. Значение магнитной восприимчивости жидкого кислорода χ=3,4·10-3.
Решение
Следует применить выражение, которое показывает связь напряженности магнитного поля и намагниченности, то есть:
J→=χH→.
Далее произведем поиск поля в центре витка с током, так как необходимо вычислить намагниченность в этой точке.
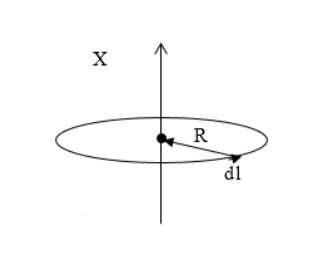
Рисунок 1
На проводнике с током необходимо выбрать элементарный участок, показанный на рисунке 1, как основу для решения задания. Применим формулу напряженности элемента витка с током.
Тогда:
dH=14πIdlsin υr2.
Где r→ – является радиус-вектором, проведенным из элемента тока в рассматриваемую точку,
dl→ – элемент проводника с током, υ – угол между dl→ и r→.
Опираясь на рисунок 1, υ=90°, следует упрощение J→=χH→. Так как расстояние от центра окружности элемента проводника с током постоянно и равняется радиусу витка R, получаем:
dH=14πIdlR2.
Направление результирующего вектора напряженности магнитного поля совпадает с осью Х. Его находят как сумму отдельных векторов dH→, потому что все элементы тока создают в центре витка магнитные поля, которые направлены вдоль нормали витка. Используя принцип суперпозиции, полная напряженность магнитного поля находится при переходе к интегралу вида:
H=∮dH.
Произведем подстановку dH=14πIdlR2 в H=∮dH:
H=14πIR2∮dl=14πIR22πR=12IR.
Для нахождения намагниченности, следует подставить значение напряженности из H=14πIR2∮dl=14πIR22πR=12IR в J→=χH→. тогда:
J=χ2IR.
Вычисляем с числовыми выражениями:
J=3,4·10-32·20,1=3,4·10-2 Ам.
Ответ: J=3,4·10-2 Ам.
Пример 2
Произвести вычисление доли суммарного магнитного поля в вольфрамовом стержне, находящегося во внешнем однородном магнитном поле, которую определяют молекулярные токи. Значение магнитной проницаемости вольфрама равняется μ=1,0176.
Решение
Нахождение индукции магнитного поля B’, приходящейся на долю молекулярных токов, представляется:
B’=μ0J, где J – является намагниченностью. Ее связь с напряженностью выражается через соотношение:
J=χH.
Магнитная восприимчивость находится из
χ=μ-1.
Магнитное поле молекулярных токов будет равно:
B’=μ0(μ-1)H.
По формуле находим полное поле в стержне:
B=μμ0H.
Задействовав выражения B’=μ0(μ-1)H, B=μμ0H, найдем соотношение:
B’B=μ0(μ-1)Hμμ0H=μ-1μ.
Подставим числовые выражения:
B’B=1,0176-11,0176=0,0173.
Ответ:B’B=0,0173.
Разделение веществ
В пятидесятые годы девятнадцатого столетия Фарадей исследовал влияние веществ на МП. В итоге он пришёл к выводу, что все материалы без исключения влияют на поле. Отсюда следует, что любое вещество является источником своего МП, но при условии его помещения во внешнее поле. Это явление было названо намагниченностью.
По результатам своего исследования Фарадей разделил все физические элементы на три класса, дав определение каждому из них:

- Диамагнетики. Вещества, у которых проницаемость чуть меньше единицы: μ < 1. К ним относятся все газы, кроме кислорода, золота, серебра, углерода в любой кристаллической модификации, висмута. При помещении этих веществ в МП собственный вектор магнитной индукции направлен в сторону противоположную вектору, создаваемому током: B1↑↓B0. C другой стороны, так как значение B1 близко к единице, то модуль вектора B1 гораздо меньше модуля B0. Получается, что такое вещество намагничивается очень слабо и против внешнего поля. Интересным фактом является то, что диамагнетики при помещении в катушку с МП выталкиваются из неё.
- Парамагнетики. К ним относят материалы, у которых магнитная проницаемость немного больше единицы. Например, щелочные металлы, алюминий вольфрам, магний, платина. Для этих веществ характерно то, что модуль B1 параллелен вектору B0, но при этом модуль B1 меньше, чем модуль вектора B0.
- Ферромагнетики. К этому классу относят материалы, у которых μ намного больше единицы. Классическими представителями таких веществ являются: железо, никель, кобальт и их сплавы. Эти вещества намагничиваются вдоль поля. При этом B1 по модулю гораздо больше B0. Такие материалы сильно увеличивают магнитное поле.
В однородном МП на тело, обладающее магнитным моментом, действует только момент сил, который стремится развернуть диполь вдоль направления силовых линий. В неоднородном поле на диполь будет дополнительно действовать сила, пропорциональная величине дипольного момента и градиента поля: F = P (dB/dn) * cosj.
Если момент ориентирован вдоль линий, то на него действует сила притяжения. В ином случае он отталкивается, что и характерно для диамагнетиков.
Гипотеза Ампера
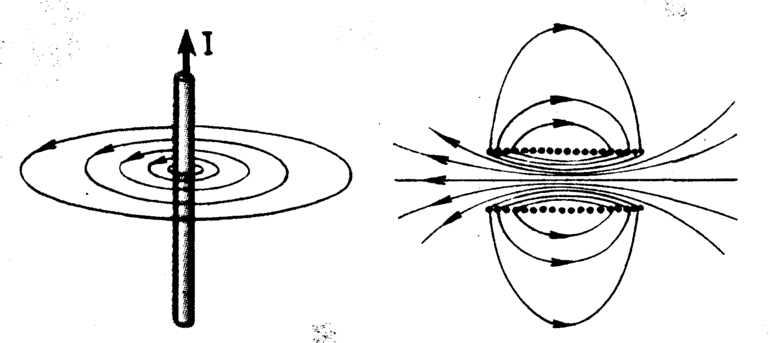
С её помощью можно объяснить, почему одни вещества проявляют парамагнитные или диамагнитные свойства, а другие усиливают МП. Ампер провёл ряд экспериментов, сравнивая конфигурацию поля, создаваемого полосовым магнитом и катушкой с током. Было определено, что для полосового магнита характерна ситуация, когда линии потока выходят из северного полюса и входят в южный. Катушка же создаёт поле, похожее на конфигурацию МП постоянного полосового магнита.
Это сходство позволило Амперу предположить, что магнитные свойства веществ обусловлены тем, что внутри их существует своя проводимость, которая может убывать или возрастать в зависимости от внешних воздействующих факторов. Так, Ампер утверждал, что магнитные свойства материала объясняются существованием в его объёме микроскопических замкнутых электрических токов. Впоследствии его догадка была подтверждена. Такие токи названы молекулярными.
Другими словами, это электроны, движущиеся вокруг ядра в атоме. Для примера стоит рассмотреть гелий. В нём два электрона движутся по практически одинаковым орбитам, но только в противоположные стороны. Каждый из электронов несёт электрический заряд, создающий ток, следовательно, и поле. Если нарисовать их магнитные поля, то можно увидеть, что их направление будет противоположным: B1 + B2 = 0. Значит, атом гелия не создаёт вокруг себя МП. При помещении его во внешнее МП B0 к силе притяжения электрона прибавится сила Лоренца, направленная по радиусу от ядра.
Таким образом, сила притяжения к ядру ослабеет. Чтобы двигаться по той же самой орбите, электрону нужна меньшая скорость. Применительно ко второму электрону ситуация будет противоположной. Скорость электрона станет больше. В результате поле, создаваемое первым электроном, станет меньше, а вторым — больше. Следовательно, B1 + B2 ≠ 0. При этом гелий будет намагничиваться против внешнего поля, то есть является диамагнетиком.

Для парамагнетиков характерно то, что каждый атом обладает своим орбитальным полем. То есть атомы можно представить как витки с током. Если поля нет, направление электронов хаотичное. Причём их сумма будет равняться нулю. При помещении его во внешнее МП каждый свободный атом будет стремиться развернуться так, чтобы его нормаль была направлена по полю. Но при этом процессу мешает тепловое движение.
Поэтому полностью развернуться в сторону направления МП атомы не могут. При этом чем больше температура тела, тем меньше будет их разворот. Значит, магнитная проницаемость будет уменьшаться.
Ферромагнетики.
Самые сильные магнитные свойства проявляют ферромагнетики. Магнитные поля, которые создаваются ферромагнетиками, гораздо сильнее внешнего намагничивающего поля. Правда, магнитные поля ферромагнетиков создаются не вследствие обращения электронов вокруг ядер — орбитального магнитного момента, а вследствие собственного вращения электрона — собственного магнитного момента, называемого спином.
Температура Кюри (Тс) — это температура, выше которой ферромагнитные материалы теряют свои магнитные свойства. Для каждого ферромагнетика она своя. Например, для железа Тс= 753 °С, для никеля Тс = 365 °С, для кобальта Тс = 1000 °С. Существуют ферромагнитные сплавы, у которых Тс < 100 °С.
Первые детальные исследования магнитных свойств ферромагнетиков были выполнены выдающимся русским физиком А. Г. Столетовым (1839-1896).
Ферромагнетики применяются довольно широко: в качестве постоянных магнитов (в электроизмерительных приборах, громкоговорителях, телефонах и так далее), стальных сердечников в трансформаторах, генераторах, электродвигателях (для усиления магнитного поля и экономии электроэнергии). На магнитных лентах, которые изготовлены из ферромагнетиков, осуществляется запись звука и изображения для магнитофонов и видеомагнитофонов. На тонкие магнитные пленки производится запись информации для запоминающих устройств в электронно-вычислительных машинах.
Свойство ферромагнетиков
С точки зрения физики наиболее интересным материалом является ферромагнетик. Существует устройство, представляющее собой кольцо из него. На прибор равномерно в один слой намотан провод, через который протекает электрический ток. В этом торе возникает электрическое поле, совпадающее по величине с вектором МП. В результате сердечник окажется намагниченным.
Если по оси ординат отложить магнитную индукцию тела, а по оси — абсцисс тока, то можно обнаружить следующие особенности:
- в начальный момент времени график будет возрастать примерно под углом 30 градусов;
- после достижения определённой величины (1 Тл) произойдёт резкое выравнивание графика относительно B0.
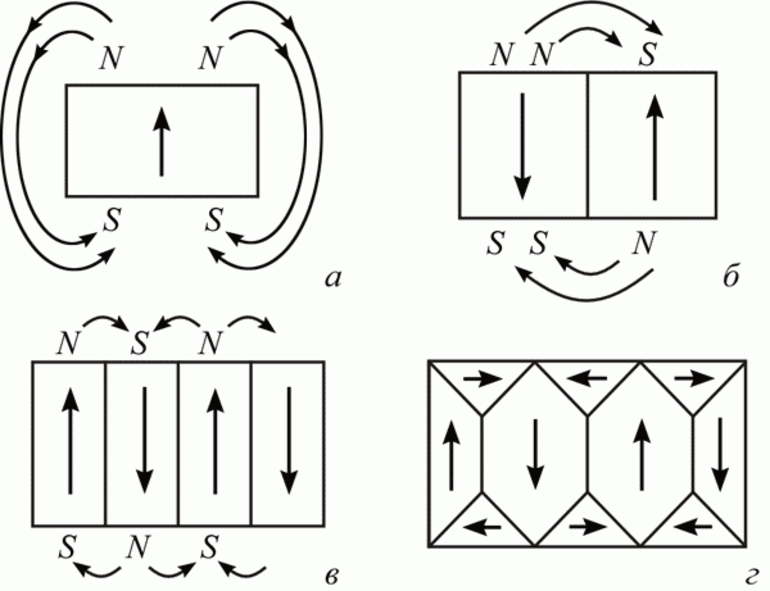
Из этого можно сделать вывод, что ферромагнетик примерно в тысячу раз увеличивает магнитное поле. Выходит, что магнитная проницаемость зависит от намагничивающего поля. Если провести перпендикуляры с точки перехода графика на координатные прямые и нарисовать из неё диагональ к нулевой точке, то тангенс угла к B0 будет равняться проницаемости: μ = tg j. Оказывается, что при больших намагничивающих полях МП перестаёт расти, то есть существует магнитное насыщение.
Если взять феррит и намагнитить его, а поле размагнитить путём уменьшения поля, то линия размагничивания будет другой. При исчезновении внешнего поля ферромагнетик останется намагниченным.
Поэтому для его размагничивания нужно создать поле, направленное в противоположную сторону. Таким образом, чередование намагниченности и размагниченности приведёт график к виду гистерезиса.
На петеле можно выделить две точки:
- Bo — остаточная магнитная индукция, возникающая после снятия электрического поля;
- Bc — коэрцитивная сила, индукция противоположно направленного поля.
Ферромагнетики, которые обладают широким гистерезисом, называются жёсткими. К ним относится закалённая сталь, сплавы альнико и магнико, неодим. Но бывают и ферромагнетики, которые довольно легко перемагнитить. Их петля гистерезиса имеет узкий вид. Используют такие материалы в электродвигателях, трансформаторах. Их называют мягкими. Примеры — отожжённая сталь, пермаллой.
Магнитометр. Что это такое?
Как следует уже из самого названия, магнитометр – это прибор, предназначенный для измерения параметров магнитного поля и магнитных свойств отдельных материалов. В зависимости от того изменения показателей какого рода фиксирует устройство, его могут называть следующими терминами:
- эрстедметр (меряет напряженность поля);
- градиентометр (определяет полевой градиент);
- тесламетр (показывает индукцию);
- веберметр (определяет магнитный поток);
- инклинатор или деклинатор (устанавливает направление поля);
- коэрцитиметр (показывает коэрцитивную силу).

Когда работают мю-метры и каппа-метры, можно выяснить соответственно магнитную проницаемость и магнитную восприимчивость. А также существуют приборы для фиксации магнитного момента. Но есть и более узкое определение магнитометров – это аппараты, замеряющие напряженность, градиент и направление поля. Определение необходимых параметров производится различными способами.
Необходимо учитывать, что одни приборы фиксируют абсолютные значения полевых характеристик, а другие отражают изменение поля с течением времени или в разных точках пространства.
Принцип работы.
Схема магнитометра может сильно отличаться, но в любом случае он работает по одной и той же методике. Магнитное поле может быть охарактеризовано следующим:
- вектор напряженности;
- горизонтальная составляющая напряженности;
- магнитное склонение;
- магнитное наклонение.


Но есть еще одна важная характеристика магнитного поля – магнитная индукция. По направлению ее вектора определяется направление силы, воздействующей на северный полюс магнита. Чтобы понять, как все это работает, полезно рассмотреть устройство магнитометрического датчика HMC5883L от Honeywell. Меняющийся коэффициент усиления влияет на восприимчивость датчика. Для считывания данных предусмотрено 12 регистров с разрядностью 8.
Регистр режима задает основной сценарий действия: непрерывное измерение либо разовый замер и переход в режим ожидания. Если запрос идет не программно, а аппаратно, используется дублирование данных через вывод DRDY. Но не все так просто – требуется учитывать не только показания датчиков, но и воздействия на них различных помех.
Если проигнорировать этот момент, может оказаться так, что модуль сбился и измеряет совсем не то, что нужно.

Предположим, требуется произвести измерения удельной намагниченности насыщения. Образец, который нужно исследовать, и постоянный магнит крепятся на тонком стержне, соединенном с вибрационным узлом. Колебания стержня могут происходить с различной частотой, но в любом случае под углом 90 градусов к полю, создаваемому электромагнитом. Радиотехнические компоненты системы призваны усиливать, очищать и эффективно обрабатывать сигнал. Когда постоянный магнит и образец колеблются, появляется электродвижущая сила в особых катушках. Сами катушки позиционируют по отношению к постоянному магниту так, чтобы на их положение не влияли вибрационные колебания.
Но описанное устройство, как нетрудно понять по некоторым моментам, может применяться преимущественно в лабораторных условиях. Возможности его использования «в поле» существенно ограничены. Для полевых измерений предназначены уже совершенно другие магнитометры, которые не требуют изготовления и выделения образцов. Как именно работает такая техника – коммерческая тайна производителей. В любом случае, нужно ли производить измерения остаточной намагниченности или делать что-то еще, важно знать алгоритм калибровки методом наименьших квадратов.


Максимально упрощенно излагая суть этого метода (основанного на высшей математике), можно указать, что он подразумевает подбор функции, дающей значения, максимально близкие к полученным по итогам эксперимента. Сумма квадратов отклонений во всех критических важных точках должна быть как можно меньшей, в идеале – сведенной к нулю.
Обязательным условием для применения такого алгоритма является знание вектора магнитного поля земли. Если же вернуться к математической стороне дела, то можно сказать, что тут нужны линейные преобразования матриц в трехмерном пространстве. А отсюда следует, что придется использовать показания по трем осям сразу.
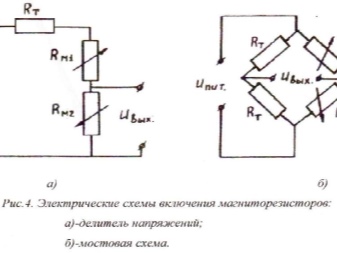
Немного отстранившись от всей этой зауми, можно разобраться, как действует магнитометр на основе тонкопленочных магниторезисторов. Такая техника выпускается ведущими иностранными фирмами. Магниторезисторы обычно размещают на одной кремниевой подложке и соединяют мостовым способом.
Поскольку сопротивление резисторов сложно подогнать при производстве, нельзя игнорировать напряжение смещения. Параметры датчиков очень сильно зависят от фактической температуры.

История
Константа была определена для упрощения выражения теоремы Ампера .
Имена и символ
Магнитная постоянная , кажется , более известный под своими старыми именами вакуумной магнитной проницаемости и вакуумной проницаемости . Старые обозначения магнитной проницаемости свободного пространства или проницаемости свободного пространства сейчас используются редко.
Обозначение константы — μ 0 (читается как «мю ноль» ). Он состоит из греческой буквы мю , за которой следует индекс ноль . Греческая буква мю — символ магнитной проницаемости. Индекс 0 означает «в вакууме» и указывает, что магнитная проницаемость μ 0 соответствует вакууму.
Размер и единица измерения
Измерение от магнитной проницаемости является [ μ 0 ] = [ μ ] = М л Т -2 Я -2 . В Международной системе единиц он выражается в Генри на метр ( Гм – 1 ), единицей, производной от магнитной проницаемости.
Физическая интерпретация
Магнитная проницаемость μ материала определяется как отношение между нормой магнитной индукции поля В и что из магнитного поля возбуждения Н , приложенного к материалу. Для достаточно больших полей это отношение непостоянно и стремится к μ 0 .
μ 0 можно рассматривать как собственную магнитную проницаемость вакуума .
