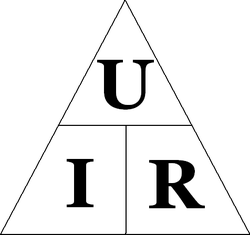
Мнемоническая диаграмма для закона Ома
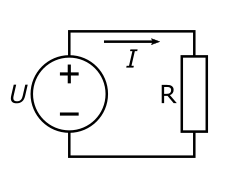
Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.png/250px-Zakon_Oma_(pererisovannyj).png)
U — электрическое напряжение;
I — сила тока;
P — электрическая мощность;
R — электрическое сопротивление
В соответствии с этой диаграммой формально может быть записано выражение:
R=UI,(7){displaystyle R!={U over I},qquad (7)}
которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.
В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:
R=ϱls,(8){displaystyle R!={varrho l over s},qquad (8)}
где:
- ϱ{displaystyle varrho }
— удельное электрическое сопротивление материала, из которого сделан проводник, - l{displaystyle l}
— его длина - s{displaystyle s}
— площадь его поперечного сечения
Закон Ома в дифференциальной форме
Сопротивление R{displaystyle R}
зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
J=σE,{displaystyle mathbf {J} =sigma mathbf {E} ,}
где:
- J{displaystyle mathbf {J} }
— вектор плотности тока, - σ{displaystyle sigma }
— удельная проводимость, - E{displaystyle mathbf {E} }
— вектор напряжённости электрического поля.
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость σij{displaystyle sigma _{ij}}
является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид
Ji=∑i=13σijEj.{displaystyle J_{i}=sum _{i=1}^{3}sigma _{ij}E_{j}.}
Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред.
Закон Ома для участка цепи
Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.
I = U/R
Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.
Отсюда следуют ещё два полезных соотношения:
Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).
U = IR
Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.
R = U/I
Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R.
Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.
Предлагается простой Онлайн-калькулятор для практических расчётов.
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности.
После сброса ввести два любых известных параметра.
| I=U/R; U=IR; R=U/I; P=UI P=U²/R; P=I²R; R=U²/P; R=P/I² U=√(PR) I= √(P/R)
|
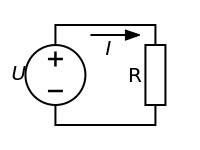
Закон Ома для замкнутой цепи
Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:
I — Сила тока в цепи.
— Электродвижущая сила (ЭДС) — величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника.
r — Внутреннее сопротивление источника питания.
Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I =
/(R+r) .
Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.
Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания.
С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U =
— I*r.
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U.
Если ток в цепи равен нулю, следовательно,
= U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС (
≈ U ) независимо от сопротивления внешней цепи R.
Такой источник питания называют источником напряжения.
Закон Ома для полной цепи
Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.
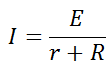
Здесь могут возникнуть вопросы. Например, что такое ЭДС?
Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает заряд.
В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.
Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.
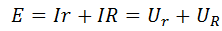
Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.
Задача 2.1
Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

Теперь решим задачу посложнее.
Задача 2.2
Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.
Приступим.

- Для постоянного тока
Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.
| I = U / R | где | I — сила тока, измеряемая в Амперах, (A) |
| U — напряжение, измеряемое в Вольтах, (V) | ||
| R — сопротивление, измеряется в Омах, (Ω) |
Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, — «Не знаешь закон Ома, — сиди дома..».
Помимо закона Ома, важнейшим является понятие электрической мощности, P:
Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.
| P = I × U | где | P — эл. мощность, измеряемая в Ваттах, (W) |
| I — сила тока, измеряемая в Амперах, (A) | ||
| U — напряжение, измеряемое в Вольтах, (V) |
Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
| Сила тока, | I= | U/R | P/U | √(P/R) |
| Напряжение, | U= | I×R | P/I | √(P×R) |
| Сопротивление, | R= | U/I | P/I² | U²/P |
| Мощность, | P= | I×U | I²×R | U²/R |
Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
Наиболее распространенные множительные приставки:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие.
Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.
Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:
— комплексная амплитуда тока.
= Iampe jφ
— комплексная амплитуда напряжения.
= Uampe jφ
— комплексное сопротивление. Импеданс.
φ — угол сдвига фаз между током и напряжением.
e — константа, основание натурального логарифма.
j — мнимая единица.
Iamp , Uamp — амплитудные значения синусоидального тока и напряжения.
Нелинейные элементы и цепи
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников.
Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы.
Такие элементы и цепи, в которых они используются, называют нелинейными.
Постоянный электрический ток. Сила тока
Электрический ток – это упорядоченное движение заряженных частиц.
Условия существования электрического тока в проводнике:
- наличие свободных заряженных частиц;
- наличие электрического поля.
Напряженность электрического поля должна быть постоянной.
Цепь постоянного тока должна быть замкнутой.
Важно!
Тепловое движение заряженных частиц нельзя назвать электрическим током, так как оно беспорядочное.
Электрический ток можно обнаружить по его действиям:
- тепловому – при протекании тока проводник нагревается;
- химическому – изменяется состав вещества при прохождении электрического тока (электролиз);
- магнитному – электрический ток создает магнитное поле.
За направление тока принимают направление движения положительно заряженной частицы.
Сила тока – это скалярная физическая величина, равная отношению заряда, прошедшего через поперечное сечение проводника, ко времени, за которое этот заряд переносится.
Обозначение – ( I ), единица измерения в СИ – ампер (А) (является основной).
Вычисляется по формуле:
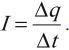
Если за одинаковые промежутки времени через поперечное сечение проводника проходит одинаковый заряд, то ток постоянный.
Для измерения силы тока используют амперметр.
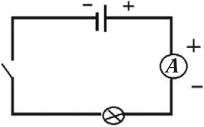
Амперметр – измерительный прибор для определения силы тока в электрической цепи.
При измерении силы тока амперметр включают в цепь последовательно с тем прибором, силу тока в котором измеряют, и с соблюдением полярности. Клемму амперметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока.
Для того чтобы включение амперметра не влияло на величину измеряемого тока, его сопротивление по сравнению с сопротивлением нагрузки должно быть как можно меньшим. Каждый амперметр рассчитывается на некоторое определенное максимальное значение измеряемой величины. Но возникают ситуации, когда необходимо выполнить измерение силы тока больше предельно допустимого значения силы тока.
Для этого параллельно амперметру присоединяют проводник (шунт), по которому проходит часть измеряемого тока. Значение сопротивления этого проводника рассчитывается так, чтобы сила тока, проходящего через амперметр, не превышала его максимально допустимого значения.
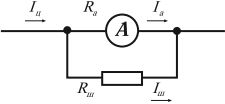
Сопротивление шунта рассчитывается по формуле:
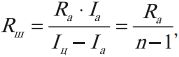
где ( I_ц ) – сила тока в цепи, ( I_а ) – максимально допустимая для данного амперметра сила тока, ( R_а ) – сопротивление амперметра, ( n=frac{I_ц}{I_а} ).
При этом цена деления прибора увеличивается в n раз, а точность измерений во столько же раз уменьшается.
Работающим с электрическими цепями надо знать, что для человеческого организма безопасной считается сила тока до 1 мА. Сила тока больше 100 мА приводит к серьезным поражениям организма.
Постоянный электрический ток. Напряжение
В проводнике, по которому протекает ток, заряды движутся под действием сил электростатического поля. Работу электростатических сил характеризуют разностью потенциалов или напряжением.
Электрическое напряжение – скалярная физическая величина, равная отношению работы по перемещению электрического заряда между двумя точками цепи к величине этого заряда.
Обозначение – ( U ), единица измерения в СИ – вольт (В).
Формула для вычисления:
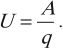
Напряжение равно разности потенциалов только в том случае, если рассматриваемый участок цепи не содержит источник тока (ЭДС = 0).
Измеряют напряжение вольтметром.
При измерении напряжения вольтметр включают в цепь параллельно с тем прибором, напряжение на котором измеряют, и с соблюдением полярности. Клемму вольтметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока. Для того чтобы включение вольтметра не влияло на измерение напряжения, его сопротивление должно быть большим.
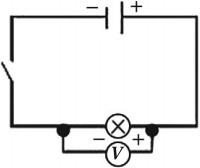
Для измерения напряжения больше, чем допустимое для данного вольтметра, используют добавочное сопротивление – резистор, включаемый последовательно с вольтметром.
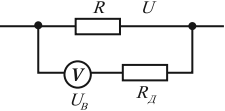
Величина добавочного сопротивления рассчитывается по формуле:
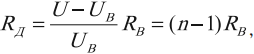
где ( U ) – напряжение, которое нужно измерить, ( U_В ) – напряжение, на которое рассчитан вольтметр, ( n=frac{U}{U_В} ), ( R_В ) – сопротивление вольтметра.
При этом цена деления прибора увеличивается в ( n ) раз, а точность измерений во столько же раз уменьшается.
Электрическое сопротивление. Удельное сопротивление вещества
Электрическое сопротивление – свойство материала проводника препятствовать прохождению через него электрического тока.
Обозначение – ( R ), единица измерения в СИ – Ом.
Объяснить наличие сопротивления можно на основе строения металлических проводников. Свободные электроны при движении по проводнику встречают на своем пути ионы кристаллической решетки и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток.
Сопротивление различных проводников зависит от материала, из которого они изготовлены, их длины, геометрической формы и температуры. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м2.
Обозначение – ( rho ), единица измерения в СИ – Ом·м.
Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 1,7·10-8 Ом·м, т. е. медный проводник длиной 1 м и сечением 1 м2 обладает сопротивлением 1,7·10-8 Ом. На практике часто используют единицу удельного сопротивления (Ом·мм2)/м.
Электрическое сопротивление проводника прямо пропорционально длине проводника и обратно пропорционально площади поперечного сечения проводника.
Формула для вычисления:
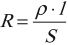
Сопротивление проводника увеличивается с ростом температуры. Удельное сопротивление зависит от температуры:
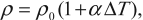
где ( rho_0 ) – удельное сопротивление при ( T_0 ) = 293 К (20°С), ( Delta T=T-T_0 ), ( alpha ) – температурный коэффициент сопротивления.
Единица измерения температурного коэффициента сопротивления – К-1.
При нагревании увеличивается интенсивность движения частиц вещества. Это создает трудности для направленного движения электронов. Увеличивается число столкновений свободных электронов с ионами кристаллической решетки.
Свойство изменения сопротивления при изменении температуры используется в термометрах сопротивления. Эти приборы могут измерять температуру, основываясь на зависимости сопротивления от температуры. У термометров сопротивления высокая точность измерений.
Основные формулы раздела «Законы постоянного тока»



Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
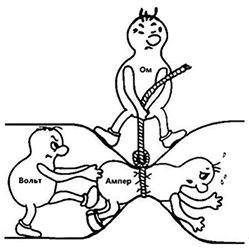
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Где и когда можно применять закон Ома?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Трактовка и пределы применимости закона Ома
Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.
В классическом приближении закон Ома можно вывести при помощи теории Друде:
J=n⋅e02⋅τm⋅E=σ⋅E.{displaystyle mathbf {J} ={frac {ncdot e_{0}^{2}cdot tau }{m}}cdot mathbf {E} =sigma cdot mathbf {E} .}
Здесь:
- σ{displaystyle sigma }
— электрическая удельная проводимость; - n{displaystyle n}
— концентрация электронов; - e0{displaystyle e_{0}}
— элементарный заряд; - τ{displaystyle tau }
— время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался); - m{displaystyle m}
— эффективная масса электрона.
Проводники и элементы, для которых соблюдается закон Ома, называются омическими.
Закон Ома может не соблюдаться:
- При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
- При низких температурах для веществ, обладающих сверхпроводимостью.
- При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
- При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
- В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
- В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
- В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике) .
- https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%9E%D0%BC%D0%B0
- https://tel-spb.ru/ohm/
- https://toe.1c-umi.ru/lekcii/lekciya_6_-_zakon_oma/
- https://www.axwap.com/kipia/docs/elektrika/zakon-oma.htm
- https://fizi4ka.ru/egje-2018-po-fizike/zakony-postojannogo-toka.html