Закон Ома в интегральной и дифференциальной форме

Понятие сопротивление доходчиво

Электрическое сопротивление — это величина, которая определяет способность проводника пропускать электрический ток. Полезно также освежить знания про электрический ток

Представить это проще всего, исходя из строения металлов.

По классической теории металл состоит из кристаллической решетки, а между структурными элементами этой решетки путешествуют свободные электроны.

Внешнее электрическое поле заставляет их перемещаться и образуется электрический ток, т.е. направленное упорядоченное движение частиц.

Решетка металла мешает им двигаться по своему объему. Электроны трутся об её узлы и не могут протиснуться. Вот это явление и образует сопротивление. Это «сила», которая мешает перемещению.

Ситуация аналогично ситечку на раковине. Вода проходит, но медленнее, чем проходила бы без ситечка.

Аналогичная ситуация присутствует во всех материалах, правда род и тип частичек может меняться. Тип строения тоже разный. Но условно можно принять, что всегда структура мешает им двигаться что в дереве, что в металле.

В некоторых телах вообще таких частичек не будет, там сопротивление бесконечное (некоторые виды резин, например).

Обратите внимание, что мы не рассматриваем тут понятие электрического тока и напряжения, т.к. это отдельные темы и если есть непонимание, обязательно напишите об этом в комментариях. Правда про электрический ток есть наше видео . Эти вещи нужно четко понимать.

Ну и из сказанного очевидно, что сопротивление будет зависеть от геометрических параметров проводника (т.е. площадь сечения S, длина l) и типа проводника (который тут описывается понятием удельное сопротивление и является табличной величиной). Ещё оно зависит от температуры (чем выше тем больше для большинства тел), но это мы совсем от самого закона уходим… Для задачек на закон Ома знаний уже вполне достаточно.

Формулировка закона Ома

В результате множества экспериментов Ом вывел зависимость, которая определяет связь между силой тока в проводнике, напряжением и тем самым сопротивлением, которое мы описали выше.

Звучит закон так: Cила тока на участке электрической цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению

Вроде как все слова тут понятные, если знать все определения. Сопротивление мы разобрали. Сила тока — это, грубо говоря, количество частичек, которое окажется в проводнике. Понятие сила тока подробно я разбирал в этой статье , обязательно прочитайте её.

Напряжение — это «поток», который эти частицы несет. Вот вроде бы всё и увязали.

Если рассматривать цепь, то сопротивление по элементам распределяется согласно их техническим характеристикам и вычисляется согласно закону Ома. Т.е. мы не можем утверждать, что на каждом элементе есть одинаковое сопротивление.

Например, если в цепи с последовательным подключением две лампочки, т омы помним что сила тока во всей цепи при таком соединении одинаковая, а вот напряжение на элементах разное. Замеряем его на точках подключения лампочек, записываем и запихиваем в закон Ома. Вот всё и посчитали :)…

Закон Ома для участка цепи

Когда закон ома записан в такой форме, как мы привели выше, то он называется закон ома для участка цепи.

Почему для участка цепи? Для участка, потому что тут не учитывается сопротивление всей цепи. Можно измерить сопротивление на каждом участке исходя из приведенных характеристик.

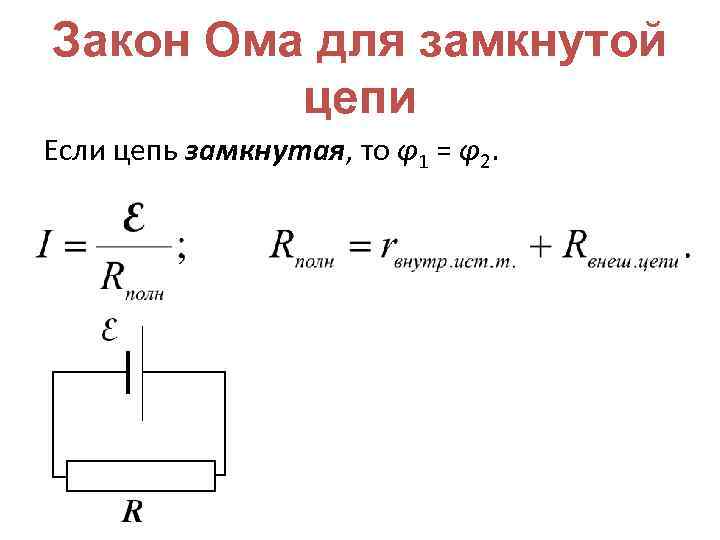
Закон Ома для полной цепи

Полной цепью (в отличие от участка цепи, применительно к которому мы излагали всё выше) называется цепь с учетом источника тока.

Почему это важно?

Именно потому, что если мы представим себе электрическую цепь условно как систему труб для воды, то участок цепи это будет незамкнутый кусок трубы, а полная цепь — зацикленная система.

Из примера может показаться, что участок цепи есть незамкнутая в электрическом смысле цепь. Нет, пример приведен не для этого. И там, и там электрическая цепь замкнута.

Просто нам нужно обозначить, что без учета источника тока и его внутреннего сопротивления (r) цепь не полная, а расчёт не всегда способен учитывать все значимые характеристики.

Ну а внутреннее сопротивление, как вы наверное догадались — это то сопротивление, которым обладает источник тока. Да, току в цепи сложно проходить и через сам источник! Даже сам источник провоцирует энергетические потери. А вот считать его аналогично расчёту для участка цепи нельзя.

Получается, что в закон Ома добавится ещё и внутренне сопротивление. И всё! Ничего страшного.

Формулировка закона Ома для полной цепи немного изменится. Теперь у нас слово напряжение заменится словом ЭДС (электродвижущая сила), а слово сопротивление заменится суммой внешнего сопротивления цепи и внутреннего сопротивления источника тока. Ну и формула будет такая:

Добавилось понятие электродвижущая сила (ЭДС), обозначенная в формуле E прописное. Что это за зверь?

ЭДС — это, по сути дела, и есть напряжение.

Разница в том, что если мы опять сравним напряжение с напором воды в водопроводе, то напряжением будет являться разница напора между двумя произвольными точками в водопроводе, а ЭДС — это напор на насосе, который качает воду.

При использовании термина ЭДС мы вспоминаем, что у источника есть внутреннее сопротивление, как оно есть и у насоса, который препятствует движению воды через самого себя. Если же мы считали бы именно напряжение источника, то мы бы приняли, что система идеальная и источник движению тока сам не препятствует.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

Для замкнутой цепи

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Следствия закона Ома.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Закон Ома в интегральной форме для неоднородного участка цепи

Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:

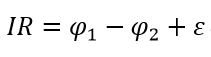
интегральный закон Ома для участка цепи

где:

• 
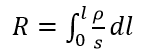
  – сопротивление участка,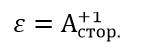
• 
  – работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи ЭДС участка,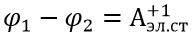
• 
  – работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи (напряжение участка),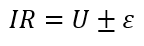
• 
  – абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи (падение напряжения участка).

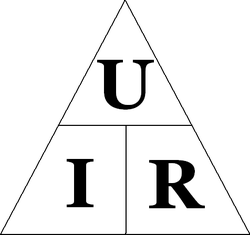
Мнемоническая диаграмма для закона Ома

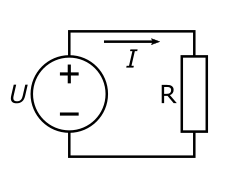
Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления
U — электрическое напряжение;
I — сила тока;
P — электрическая мощность;
R — электрическое сопротивление

В соответствии с этой диаграммой формально может быть записано выражение:

R=UI,(7){displaystyle R!={U over I},qquad (7)}

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

R=ϱls,(8){displaystyle R!={varrho l over s},qquad (8)}

где:

• ϱ{displaystyle varrho }
   — удельное электрическое сопротивление материала, из которого сделан проводник,
• l{displaystyle l}
   — его длина
• s{displaystyle s}
   — площадь его поперечного сечения

Трактовка и пределы применимости закона Ома

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

J=n⋅e02⋅τm⋅E=σ⋅E.{displaystyle mathbf {J} ={frac {ncdot e_{0}^{2}cdot tau }{m}}cdot mathbf {E} =sigma cdot mathbf {E} .}

Здесь:

• σ{displaystyle sigma }
   — электрическая удельная проводимость;
• n{displaystyle n}
   — концентрация электронов;
• e0{displaystyle e_{0}}
   — элементарный заряд;
• τ{displaystyle tau }
   — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
• m{displaystyle m}
   — эффективная масса электрона.

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
• В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике) [4] .

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

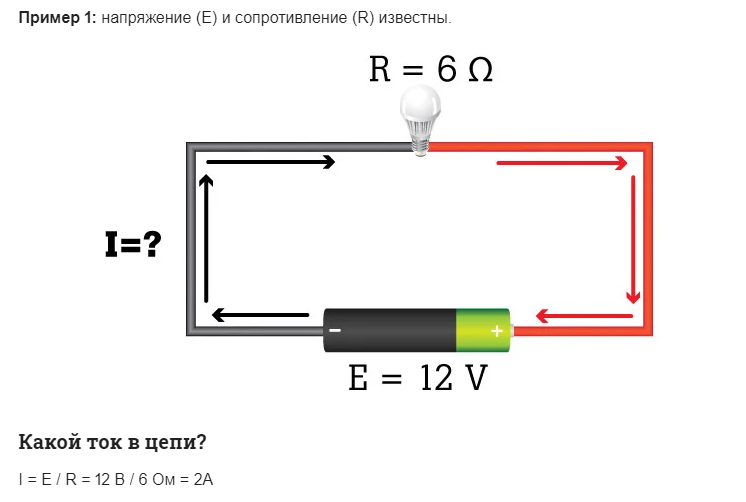
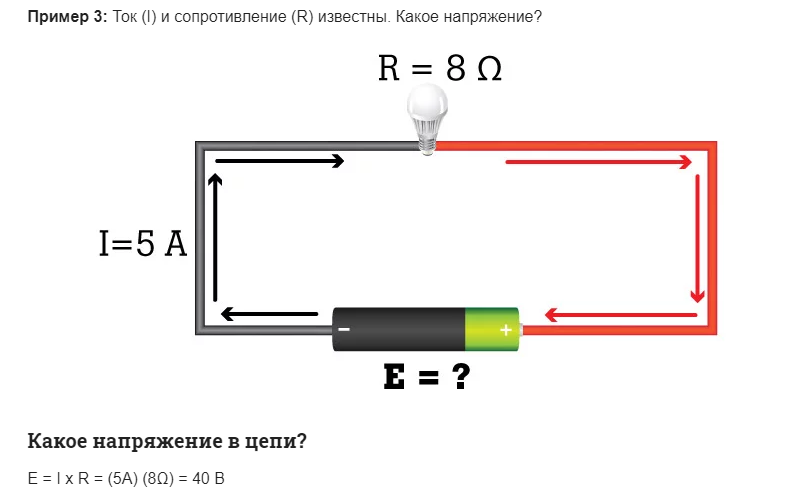
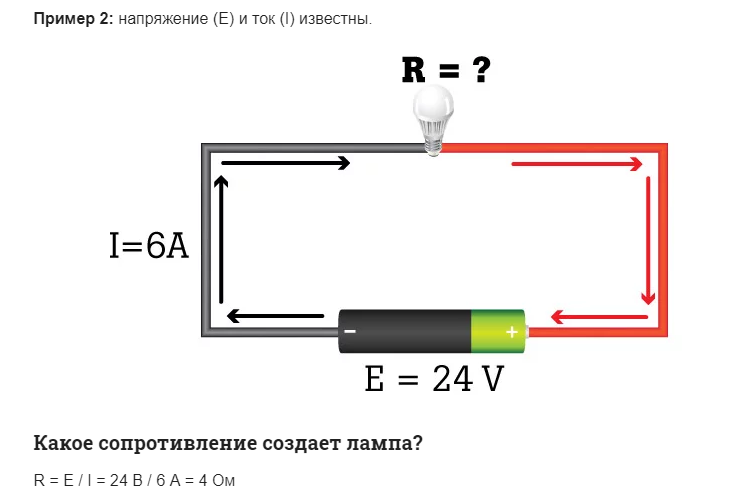
Интересно почитать: инструкция как прозвонить транзистор.

Где и когда можно применять закон Ома?

       Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

    Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.